Simply put, a real number is constructible if, starting form a line segment of unit length, a line segment of length
can be constructed with a compass and straightedge in a fintie number of steps. The study of constructible numbers is (elegantly) linked to 4 famous problems in Euclidean geometry: (1) Doubling the cube (2) Trisecting the angle (3) Squaring the circle (4) Constructing regular polygons. We will give the more detailed problem statements when looking at these problems in the second half of this post.
Here is a more rigourous definition of a constructible number. First, let us lay down the rules of the game:
- We start with two given points in the Euclidean plane, of unit length apart. These starting points are, by default, classified as constructed points.
- Given any two constructed points
and
, we may construct a (infinite) line through them using the straightedge.
- Given any three constructed points
, we may construct a circle with centre at
and radius of length
.
- The intersection points between any constructed lines and circles are considered constructed points.
A point, line, or circle is said to be constructible if they can be obtained in finitely many steps using the above rules.
Definition 1: A real number is said to be constructible if there exists two constructible points of length
apart.
Before we proceed, a quick remark about our compass. The rules above assumes that we are given a fixed compass, as opposed to a collapsing compass which collapses whenever the compass is lifted from the page. In other words, a collapsing compass cannot be used to transfer distances directly, in which case rule #3 is replaced by the following statement:
3′. Given any two constructed points , we may construct a circle with centre at
and passing through
.
However, it turns out that the use of a collapsing compass as opposed to a fixed compass is an unimportant restriction. Using a multi-step procedure, a distance can still be transferred with a collapsing compass. Interested readers may refer to Wikipedia article on the compass equivalence theorem. Henceforth, we will be using a fixed compass for simplicity.
Some basic constructions
Before we attempt to study the set of constructible numbers in detail, let us take a closer look at a couple of useful constructions that can be done with compass and straightedge. Acknowledgement: All the figures below are taken from [1].
Construction 2: Given a constructed line and a constructed point
, we can construct a line perpendicular to
and passing through
.
Proof: Obviously integer lengths are constructible. By choosing a large enough integer radius, we can get a circle centered at to intersect
at two points
. Drawing circles
of sufficiently large equal radius centered at
, the two intersection points between
yield the desired line.
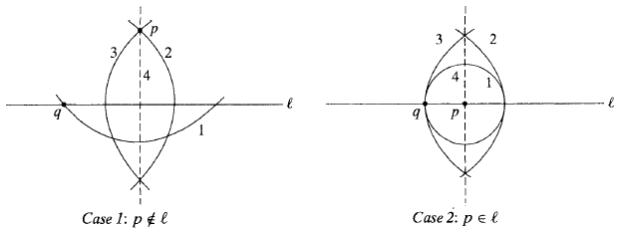
Construction 3: Given a constructed line and a constructed point
, we can construct a line parallel to
and passing through
.
Proof: First draw a line perpendicular to
passing through
, and then draw a line perpendicular to
at
.
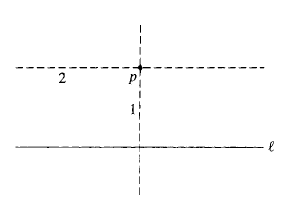
Corollary 4: The constructible numbers form a subfield of .
Proof: Given and
where
are constructed points, we need to show that
are constructible.
. Draw a circle centered at
of radius
. Let
be the point of intersection between the circle and
extended (i.e.
is between
and
). Then
.
. Draw a line perpendicular to
at
, and use the compass to mark
on this line such that
. Now, draw a line parallel to
passing through
, and use the compass to mark
on this line such that
. Finally, by using the parallel line construction, find
such that
is similar to
. Then
.
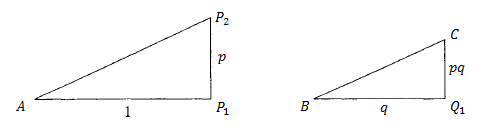
. The idea is similar as above. First construct
as before. This time, construct
such that
before using the parallel line construction to find
to complete the similar triangle. In this case,
.
Corollary 5: If is a positive constructible number, then so is
.
Proof: Let be constructed points such that
and
be on
extended such that
. By drawing circles of sufficiently large equal radius centered at
and drawing the common chord, we can find the midpoint
of
.
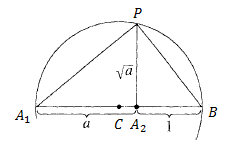
Draw the circle of radius centered at
. Draw the line perpendicular to
at
, letting
be the point of intersection with the circle. Then
(prove for similar triangles, for example).
Characterising the set of constructible numbers
Corollary 4 should give a hint that field theory would play a useful role in characterising the set of constructible numbers. Indeed, in this section we will assume some basic knowledge of field theory and describe a neat algebraic approach to understand constructible numbers.
For one direction of our characterisation, we have the following:
Theorem 6: Let be a chain of subfields of
such that
for all
. Then every element of
is constructible.
Proof: When the characteristic , a quadratic extension
is of the form
where we may assume
(this follows from the quadratic formula). Proceeding by induction along the chain, the base case
follows from corollary 4 and the observation that integers are constructible. Now assuming that every element of
is constructible, write
where
. Then
is constructible, by corollary 5. Applying corollary 4, we conclude that every element of
is constructible.
For the reverse direction, we first show the following.
Theorem 7: Suppose the two starting points have coordinates (0,0) and (1,0) and let be a constructible point. Then there exists
a chain of subfields of
with
for all
, such that the coordinates of
are in
.
Proof: To attain the point , the process requires drawing a finite sequence of lines and circles. If
are points with coordinates in a subfield
, then the line
has equation
with
If a circle has centre with coordinates in
and has radius an element of
, then the circle has equation
with
Proceeding in the spirit of induction, suppose that after drawing some number of lines and circles, all the constructed points have coordinates in a field where
is the end of a chain of quadratic extensions. In drawing the next line or circle, we see that its equation has coefficients in
as described above. Let
be a newly constructed point. We claim that the coordinates of
are in some quadratic extension of
.
- Case 1:
is the intersection between two lines. Solving two linear equations with coefficients in
gives a point with coordinates in
.
- Case 2:
is the intersection between a line and circle. Using the line equation to write one variable in terms of the other, we obtain a quadratic equation in one unknown – the desired result follows.
- Case 3:
is the intersection between two circles. The difference between the two circle equations is a linear equation. The reasoning reduces to that of case 2.
As such, a finite number of quadratic extensions will ensure that all newly constructed points due to the new line or circle have coordinates in
.
Corollary 8: Let be a constructible number. Then there exists
a chain of subfields of
with
for all
, such that
.
Proof: Suppose are constructible points such that
. By drawing a circle of radius
centered at the origin, we see that
is a constructible point. Apply theorem 7.
4 famous problems in Euclidean geometry
The algebraic approach to understanding constructible numbers yields elegant solutions to many famous geometry problems which had defied centuries of attack. The key weapon to solving these problems is the following corollary.
Corollary 9: If is constructible, then
is algebraic over
and moreover
is a power of 2.
Proof: Using the notation of corollary 8, is finite and divides
, which is a power of 2 by the multiplicative property of degree.
Without further ado, let us look at the four famous construction problems mentioned at the beginning of this post.
Problem 10: (Doubling the cube) Using only a compass and straightedge, is it possible to a construct the edge of a second cube whose volume is double that of the given first?
Solution: The problem is equivalent to asking whether is constructible. Clearly,
satisfies
which is irreducible (e.g. by Eisenstein’s criterion). As such,
which is not a power of 2. The answer is no.
Problem 11: (Trisecting the angle) Using only a compass and straightedge, is it possible, given two lines meeting at an arbitrary angle , to construct a two lines meeting at angle
?
Solution: Assume on the contrary that it is possible, in particular for the choice .
Now, starting with the points and
, it is easy to construct an equilateral triangle of unit side length. By assumption, we can construct two lines
that meet at
at angle
. By constructing
on
such that
and drawing the line perpendicular to
passing through
, we are able to construct the length
.
From the triple angle formula , we know that
satisfies the polynomial
, which is irreducible (e.g. using the rational root theorem). This yields the desired contradiction with corollary 9.
Problem 12: (Squaring the circle) Using only a compass and straightedge and given a circle, is it possible to construct a square with the same area?
Solution: Assume on the contrary that it is possible. Starting with the points and
, we are able to draw a circle with radius
and hence by assumption
is constructible. By corollary 9, this implies that
is algebraic and hence
is algebraic but
is transcendental (see previous post on transcendental numbers).
Problem 13: (Constructing regular polygons) Using only a compass and straightedge and given two starting points, is it possible to construct a regular -gon for any
?
Solution: We will focus on the case where is an odd prime
and give a necessary condition for a regular
-gon to be constructible.
As the exterior angle to a regular -gon is
, we deduce that
is constructible. Let
. Since
, we have the following field extension:
It is well-known from basic field theory that the minimal polynomial of is
and so
. At the same time,
because
satisfies the equation
and . As such,
By corollary 9, we conclude that is a power of 2, i.e.
is of the form
. More specifically,
needs to be a power of 2 as well – if
has an odd factor
, then writing
, we can factorize
as
which is a contradiction. Therefore, must be of the form
, i.e.
is a Fermat prime.
Remark: It turns out that the condition of being a Fermat prime is also sufficient for the constructibility of the regular
-gon. This was shown by Gauss. More generally, a regular
-gon is constructible if and only if
is a product of a power of 2 and any number of distinct Fermat primes (including none). This is known as the Gauss-Wantzel theorem.
References
[1] Artin, M. (2010). Algebra. (2nd ed.). Prentice Hall.
[2] Milne, J.S. (2017). Fields and Galois Theory. (Version 4.53). http://www.jmilne.org/math/CourseNotes/FT.pdf
[3] Wikipedia. Constructible number. https://en.wikipedia.org/wiki/Constructible_number